Submitted by LOGOS - Overseer on
Submitted by LOGOS - Overseer on
The basic tenant of metaphysic teaches us that energy responds to intention. Once our intention is set upon healing another person not only do we become a conduit for healing but the energy of the crystals and stones we are using also pick up the vibration of the healing intention bringing forth their own inherent and special healing gifts.
Nature is filled with Sacred Geometry and the Mineral Kingdom is no exception. Crystalline structures can be thought of as the Earth’s DNA storing the evolution of the planet. Science tells us that crystals formed from the same mineral or combination of minerals can crystallize differently. The outward expression of a crystal is based upon its internal order although the outer form may not always reflect what is going on at the heart or core of the crystal. At the inner most center of a crystal is its atomic structure spinning or rotating at a particular frequency or vibration. This represents the energy of a crystal and is what a sensitive person feels when handling a crystal. It should be remembered that stones and crystals share the same electromagnetic patterning and atomic structure as the Earth, the human body, and all other creatures and entities. Surrounding the center is Sacred Geometry as chosen by Nature upon which the crystal is built. This internal structure is believed to be constant and unchanging.
“In mineralogy and crystallography, a crystal structure is a unique arrangement is a unique arrangement of atoms in a crystal. A crystal structure is composed of a unit cell, a set of atoms arranged in a particular way; which is periodically repeated in three dimensions on a lattice. The spacing between unit cells in various directions is called its lattice parameters. The symmetry properties of the crystal are embodied in its space group. A crystal's structure and symmetry play a role in determining many of its properties, such as cleavage, electronic band structure, and optical properties.” - Wikipedia
There are six crystal systems that delineate their symmetry - Isometric, Orthorhombic, Tetragonal, Monoclinic, Hexagonal, and Triclinic.
ISOMETRIC – block like or ball like with many similar symmetrical faces forming as cubes, octahedrons and dodecahedrons. Sodalite, Fluorite, Garnet, Lapis, Galena, and Pyrite are a few examples.
ORTORHOMBIC – short stubby diamond shaped or rectangular at the cross section forming as four sided prisms, pyramids and pinacoids (an open form with two parallel faces). Examples are Sulphur, Cat’s Eye, Peridot, Topaz, and Marcasite.
TETRAGONAL – long, slender, and needle like forming as four sided prisms, pyramids, and dipyramids. Examples are Rutile, Cassiterite, Apophyllite, and Zircon.
MONOCLINIC – stubby with tilted matching faces at opposite ends forming as prisms and pinacoids. Examples are Malachite, Azurite, Chrysocolla, Jade, Selenite, and Serpentine.
HEXAGONAL (TRIGONAL) – prismatic or columnar with rounded triangular or hexagonal cross section forming as six sided prisms, pyramids, and rhombehedrons. Examples are Tourmaline, Beryl, Quartz, Cinnabar, Hematite, Calcite, Dioptase, and Apatite.
TRICLINIC – flat with sharp edges and a thin cross section with no right angles forming as pinacoids. Examples are Turquoise, Wulfenite, and Feldspar.
Here are the many geometric forms of crystal structure:
The Platonic Solids
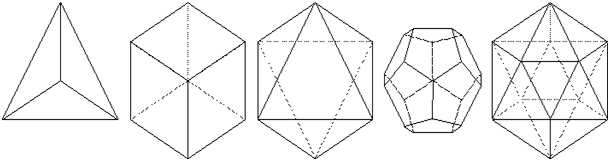
The 5 Platonic solids (Tetrahedron, Cube or (Hexahedron), Octahedron, Dodecahedron & Icosahedron) are ideal, primal models of crystal patterns that occur throughout the world of minerals in countless variations. These are the only five regular polyhedra, that is, the only five solids made from the same equilateral, equiangular polygons. To the Greeks, these solids symbolized fire, earth, air, spirit (or ether) and water respectively. The cube and octahedron are duals, meaning that one can be created by connecting the midpoints of the faces of the other. The icosahedron and dodecahedron are also duals of each other, and three mutually perpendicular, mutually bisecting golden rectangles can be drawn connecting their vertices and midpoints, respectively. The tetrahedron is a dual to itself.
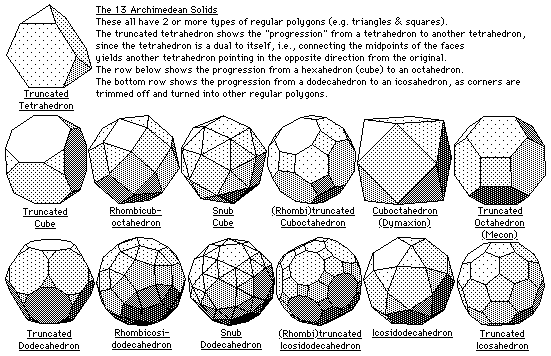
The Archimedean Solids
There are 13 Archimedean solids, each of which is composed of two or more different regular polygons. Interestingly, 5 (Platonic) and 13 (Archimedean) are both Fibonacci numbers, and 5, 12 and 13 form a perfect right triangle.
Forms, Open and Closed
Any group of crystal faces related by the same symmetry is called a form. There are 47 or 48 crystal forms depending on the classification used.
Closed forms are those groups of faces all related by symmetry that completely enclose a volume of space. It is possible for a crystal to have entirely faces of one closed form. Open forms are those groups of faces all related by symmetry that do not completely enclose a volume of space. A crystal with open form faces requires additional faces as well. There are 17 or 18 open forms and 30 closed forms.
Triclinic, Monoclinic and Orthorhombic Forms
Pedion - A single face unrelated to any other by symmetry. Open
Pinacoid - A pair of parallel faces related by mirror plane or twofold symmetry axis. Open
Dihedron - A pair of intersecting faces related by mirror plane or twofold symmetry axis. Some crystallographers distinguish between domes (pairs of intersecting faces related by mirror plane) and sphenoids (pairs of intersecting faces related by twofold symmetry axis). All are open forms.
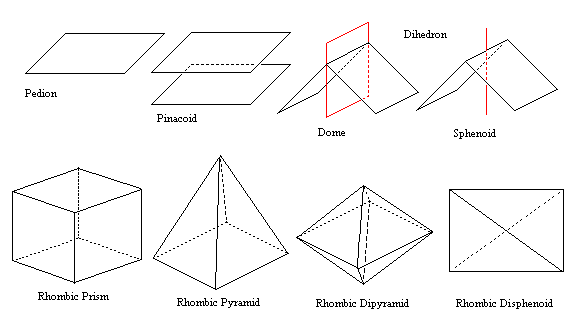
3-, 4- and 6-Fold Prisms
Prism - A collection of faces all parallel to a symmetry axis. All are open.
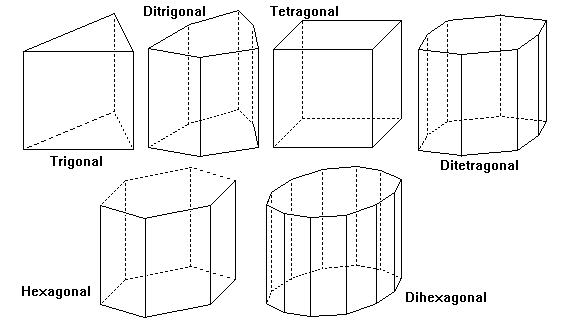
3-, 4- and 6-Fold Pyramids
Pyramid - A group of faces intersecting at a symmetry axis. All are open. The base of the pyramid would be a pedion.
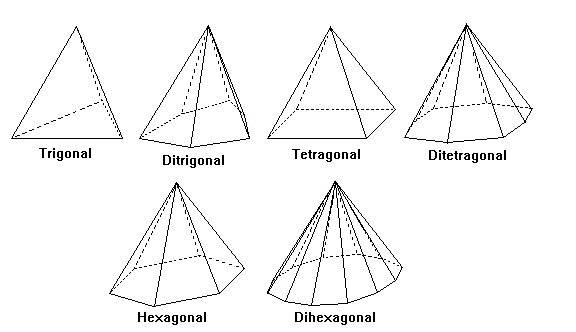
3-, 4- and 6-Fold Dipyramids
Dipyramid -Two pyramids joined base to base along a mirror plane. All are closed, as are all following forms.

Scalenohedra and Trapezohedra
Disphenoid - A solid with four congruent triangle faces, like a distorted tetrahedron. Midpoints of edges are twofold symmetry axes. In the tetragonal disphenoid the faces are isoceles triangles and a fourfold inversion axis joins the midpoints of the bases of the isoceles triangles.
Scalenohedron - A solid made up of scalene triangle faces (all sides unequal)
Trapezohedron - A solid made of trapezia (irregular quadrilaterals)
Rhombohedron - A solid with six congruent parallelogram faces. Can be considered a cube distorted along one of its diagonal three-fold symmetry axes.
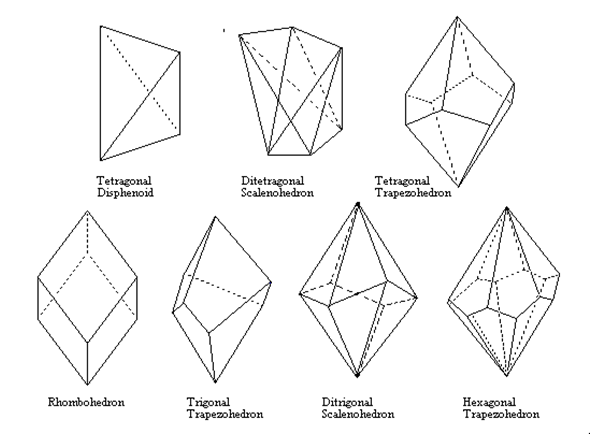
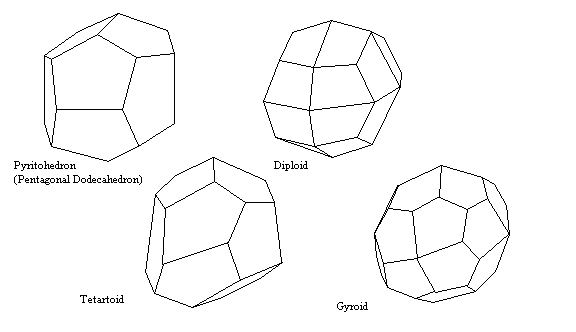
Tetartoidal, Gyroidal and Diploidal Forms
Tetartoid - 12 congruent irregular pentagonal faces. The name comes from a Greek root for one-fourth because only a quarter of the 48 faces for full isometric symmetry are present.
Tetartoid - 12 congruent irregular pentagonal faces. The name comes from a Greek root for one-fourth because only a quarter of the 48 faces for full isometric symmetry are present.
Gyroid - 24 congruent irregular pentagonal faces.
Diploid - 24 congruent irregular quadrilateral faces. The name comes from a Latin root for half, because half of the 48 faces for full isometric symmetry are present.
Pyritohedron - Faces are each perpendicular to a mirror plane, reducing the number of faces to 12 pentagonal faces. Although this superficially looks like the Platonic solid with 12 regular pentagon faces, these faces are not regular.
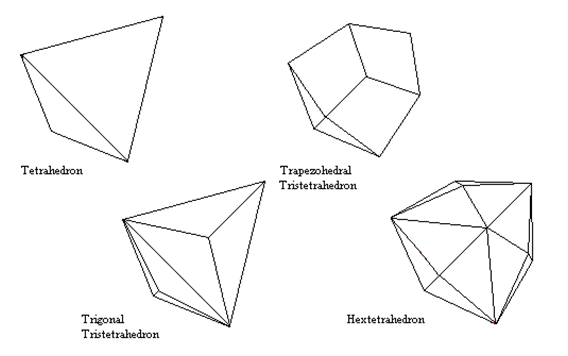
Hextetrahedral Forms
Tetrahedron - Four equilateral triangle faces.
Trapezohedral Tristetrahedron - 12 kite-shaped faces.
Trigonal Tristetrahedron - 12 isoceles triangle faces. Like a tetrahedron with a low triangular pyramid built on each face.
Hextetrahedron - 24 triangular faces.
Hexoctahedral Forms
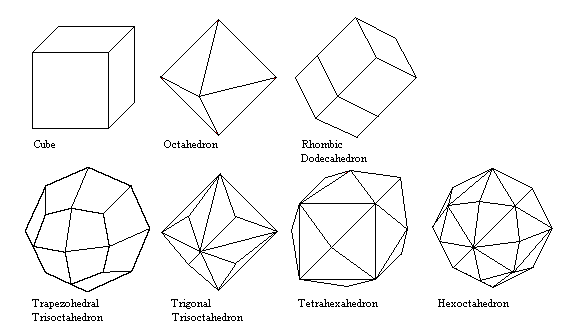
Cube - Six square faces.
Octahedron – Eight equilateral triangle faces.
Rhombic Dodecahedron - 12 rhombic faces.
Trapezohedral Trisoctahedron - 24 kite-shaped faces. Note that the indices for the two trisoctahedra are the opposite of those for the tristetrahedra.
Trigonal Trisoctahedron - 24 isoceles triangle faces. Like an octahedron with a low triangular pyramid built on each face.
Tetrahexahedron - 24 isoceles triangle faces. Like a cube with a low pyramid built on each face.
Hexoctahedron - 48 triangular faces.